Unsupervised Learning using Bayesian Mixture Models
The following tutorial illustrates the use of Turing for clustering data using a Bayesian mixture model. The aim of this task is to infer a latent grouping (hidden structure) from unlabelled data.
Synthetic Data
We generate a synthetic dataset of $N = 60$ two-dimensional points $x_i \in \mathbb{R}^2$ drawn from a Gaussian mixture model. For simplicity, we use $K = 2$ clusters with
- equal weights, i.e., we use mixture weights $w = [0.5, 0.5]$, and
- isotropic Gaussian distributions of the points in each cluster.
More concretely, we use the Gaussian distributions $\mathcal{N}([\mu_k, \mu_k]^\mathsf{T}, I)$ with parameters $\mu_1 = -3.5$ and $\mu_2 = 0.5$.
using Distributions
using FillArrays
using StatsPlots
using LinearAlgebra
using Random
# Set a random seed.
Random.seed!(3)
# Define Gaussian mixture model.
w = [0.5, 0.5]
μ = [-3.5, 0.5]
mixturemodel = MixtureModel([MvNormal(Fill(μₖ, 2), I) for μₖ in μ], w)
# We draw the data points.
N = 60
x = rand(mixturemodel, N);
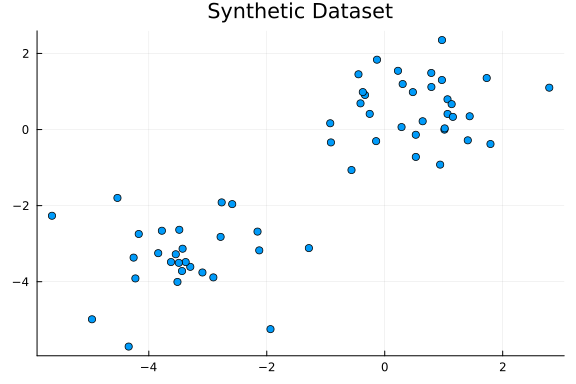
The following plot shows the dataset.
scatter(x[1, :], x[2, :]; legend=false, title="Synthetic Dataset")
Gaussian Mixture Model in Turing
We are interested in recovering the grouping from the dataset. More precisely, we want to infer the mixture weights, the parameters $\mu_1$ and $\mu_2$, and the assignment of each datum to a cluster for the generative Gaussian mixture model.
In a Bayesian Gaussian mixture model with $K$ components each data point $x_i$ ($i = 1,\ldots,N$) is generated according to the following generative process. First we draw the model parameters, i.e., in our example we draw parameters $\mu_k$ for the mean of the isotropic normal distributions and the mixture weights $w$ of the $K$ clusters. We use standard normal distributions as priors for $\mu_k$ and a Dirichlet distribution with parameters $\alpha_1 = \cdots = \alpha_K = 1$ as prior for $w$: $$ \begin{aligned} \mu_k &\sim \mathcal{N}(0, 1) \qquad (k = 1,\ldots,K)\ w &\sim \operatorname{Dirichlet}(\alpha_1, \ldots, \alpha_K) \end{aligned} $$ After having constructed all the necessary model parameters, we can generate an observation by first selecting one of the clusters $$ z_i \sim \operatorname{Categorical}(w) \qquad (i = 1,\ldots,N), $$ and then drawing the datum accordingly, i.e., in our example drawing $$ x_i \sim \mathcal{N}([\mu_{z_i}, \mu_{z_i}]^\mathsf{T}, I) \qquad (i=1,\ldots,N). $$ For more details on Gaussian mixture models, we refer to Christopher M. Bishop, Pattern Recognition and Machine Learning, Section 9.
We specify the model with Turing.
using Turing
@model function gaussian_mixture_model(x)
# Draw the parameters for each of the K=2 clusters from a standard normal distribution.
K = 2
μ ~ MvNormal(Zeros(K), I)
# Draw the weights for the K clusters from a Dirichlet distribution with parameters αₖ = 1.
w ~ Dirichlet(K, 1.0)
# Alternatively, one could use a fixed set of weights.
# w = fill(1/K, K)
# Construct categorical distribution of assignments.
distribution_assignments = Categorical(w)
# Construct multivariate normal distributions of each cluster.
D, N = size(x)
distribution_clusters = [MvNormal(Fill(μₖ, D), I) for μₖ in μ]
# Draw assignments for each datum and generate it from the multivariate normal distribution.
k = Vector{Int}(undef, N)
for i in 1:N
k[i] ~ distribution_assignments
x[:, i] ~ distribution_clusters[k[i]]
end
return k
end
model = gaussian_mixture_model(x);
We run a MCMC simulation to obtain an approximation of the posterior distribution of the parameters $\mu$ and $w$ and assignments $k$.
We use a Gibbs sampler that combines a particle Gibbs sampler for the discrete parameters (assignments $k$) and a Hamiltonion Monte Carlo sampler for the continuous parameters ($\mu$ and $w$).
We generate multiple chains in parallel using multi-threading.
sampler = Gibbs(PG(100, :k), HMC(0.05, 10, :μ, :w))
nsamples = 100
nchains = 3
chains = sample(model, sampler, MCMCThreads(), nsamples, nchains);
Inferred Mixture Model
After sampling we can visualize the trace and density of the parameters of interest.
We consider the samples of the location parameters $\mu_1$ and $\mu_2$ for the two clusters.
plot(chains[["μ[1]", "μ[2]"]]; colordim=:parameter, legend=true)

It can happen that the modes of $\mu_1$ and $\mu_2$ switch between chains. For more information see the Stan documentation for potential solutions.
We also inspect the samples of the mixture weights $w$.
plot(chains[["w[1]", "w[2]"]]; colordim=:parameter, legend=true)
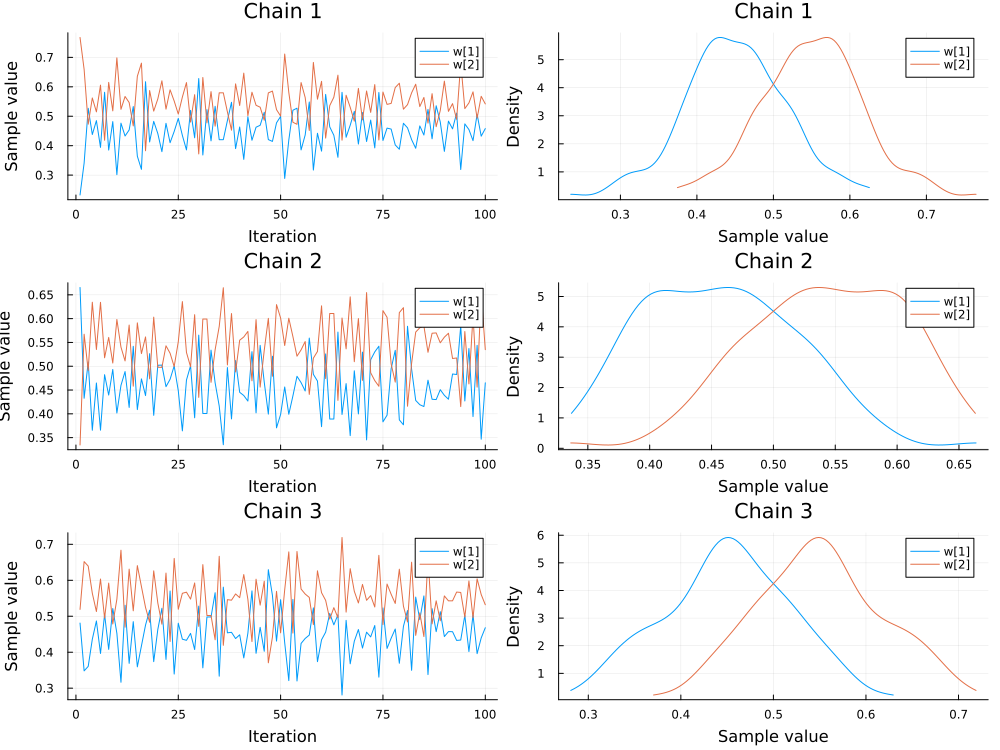
In the following, we just use the first chain to ensure the validity of our inference.
chain = chains[:, :, 1];
As the distributions of the samples for the parameters $\mu_1$, $\mu_2$, $w_1$, and $w_2$ are unimodal, we can safely visualize the density region of our model using the average values.
# Model with mean of samples as parameters.
μ_mean = [mean(chain, "μ[$i]") for i in 1:2]
w_mean = [mean(chain, "w[$i]") for i in 1:2]
mixturemodel_mean = MixtureModel([MvNormal(Fill(μₖ, 2), I) for μₖ in μ_mean], w_mean)
contour(
range(-7.5, 3; length=1_000),
range(-6.5, 3; length=1_000),
(x, y) -> logpdf(mixturemodel_mean, [x, y]);
widen=false,
)
scatter!(x[1, :], x[2, :]; legend=false, title="Synthetic Dataset")
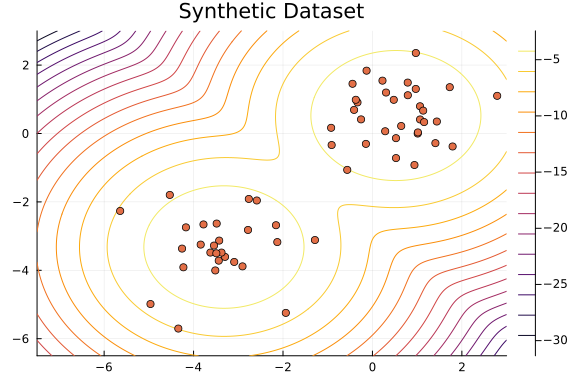
Inferred Assignments
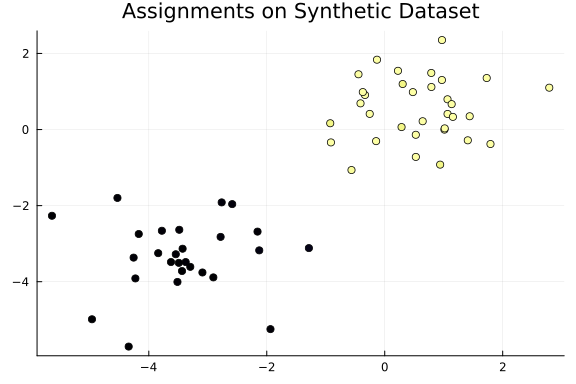
Finally, we can inspect the assignments of the data points inferred using Turing. As we can see, the dataset is partitioned into two distinct groups.
assignments = [mean(chain, "k[$i]") for i in 1:N]
scatter(
x[1, :],
x[2, :];
legend=false,
title="Assignments on Synthetic Dataset",
zcolor=assignments,
)
Appendix
These tutorials are a part of the TuringTutorials repository, found at: https://github.com/TuringLang/TuringTutorials.
To locally run this tutorial, do the following commands:
using TuringTutorials
TuringTutorials.weave("01-gaussian-mixture-model", "01_gaussian-mixture-model.jmd")
Computer Information:
Julia Version 1.9.2
Commit e4ee485e909 (2023-07-05 09:39 UTC)
Platform Info:
OS: Linux (x86_64-linux-gnu)
CPU: 128 × AMD EPYC 7502 32-Core Processor
WORD_SIZE: 64
LIBM: libopenlibm
LLVM: libLLVM-14.0.6 (ORCJIT, znver2)
Threads: 1 on 128 virtual cores
Environment:
JULIA_CPU_THREADS = 128
JULIA_DEPOT_PATH = /cache/julia-buildkite-plugin/depots/7aa0085e-79a4-45f3-a5bd-9743c91cf3da
Package Information:
Status `/cache/build/exclusive-amdci1-0/julialang/turingtutorials/tutorials/01-gaussian-mixture-model/Project.toml`
[31c24e10] Distributions v0.25.100
[1a297f60] FillArrays v1.5.0
[f3b207a7] StatsPlots v0.15.6
[fce5fe82] Turing v0.28.1
[37e2e46d] LinearAlgebra
[9a3f8284] Random
And the full manifest:
Status `/cache/build/exclusive-amdci1-0/julialang/turingtutorials/tutorials/01-gaussian-mixture-model/Manifest.toml`
[47edcb42] ADTypes v0.1.6
[621f4979] AbstractFFTs v1.5.0
[80f14c24] AbstractMCMC v4.4.2
⌅ [7a57a42e] AbstractPPL v0.5.4
[1520ce14] AbstractTrees v0.4.4
[79e6a3ab] Adapt v3.6.2
[0bf59076] AdvancedHMC v0.5.3
[5b7e9947] AdvancedMH v0.7.5
[576499cb] AdvancedPS v0.4.3
[b5ca4192] AdvancedVI v0.2.4
[dce04be8] ArgCheck v2.3.0
[7d9fca2a] Arpack v0.5.4
[4fba245c] ArrayInterface v7.4.11
[a9b6321e] Atomix v0.1.0
[13072b0f] AxisAlgorithms v1.0.1
[39de3d68] AxisArrays v0.4.7
[198e06fe] BangBang v0.3.39
[9718e550] Baselet v0.1.1
⌅ [76274a88] Bijectors v0.12.8
[d1d4a3ce] BitFlags v0.1.7
[fa961155] CEnum v0.4.2
[49dc2e85] Calculus v0.5.1
[082447d4] ChainRules v1.53.0
[d360d2e6] ChainRulesCore v1.16.0
[9e997f8a] ChangesOfVariables v0.1.8
[aaaa29a8] Clustering v0.15.4
[944b1d66] CodecZlib v0.7.2
[35d6a980] ColorSchemes v3.23.0
[3da002f7] ColorTypes v0.11.4
[c3611d14] ColorVectorSpace v0.10.0
[5ae59095] Colors v0.12.10
[861a8166] Combinatorics v1.0.2
[38540f10] CommonSolve v0.2.4
[bbf7d656] CommonSubexpressions v0.3.0
[34da2185] Compat v4.9.0
[a33af91c] CompositionsBase v0.1.2
[f0e56b4a] ConcurrentUtilities v2.2.1
[88cd18e8] ConsoleProgressMonitor v0.1.2
[187b0558] ConstructionBase v1.5.3
[d38c429a] Contour v0.6.2
[a8cc5b0e] Crayons v4.1.1
[9a962f9c] DataAPI v1.15.0
[864edb3b] DataStructures v0.18.15
[e2d170a0] DataValueInterfaces v1.0.0
[244e2a9f] DefineSingletons v0.1.2
[8bb1440f] DelimitedFiles v1.9.1
[b429d917] DensityInterface v0.4.0
[163ba53b] DiffResults v1.1.0
[b552c78f] DiffRules v1.15.1
[b4f34e82] Distances v0.10.9
[31c24e10] Distributions v0.25.100
[ced4e74d] DistributionsAD v0.6.52
[ffbed154] DocStringExtensions v0.9.3
[fa6b7ba4] DualNumbers v0.6.8
⌃ [366bfd00] DynamicPPL v0.23.0
[cad2338a] EllipticalSliceSampling v1.1.0
[4e289a0a] EnumX v1.0.4
[460bff9d] ExceptionUnwrapping v0.1.9
[e2ba6199] ExprTools v0.1.10
[c87230d0] FFMPEG v0.4.1
[7a1cc6ca] FFTW v1.7.1
[1a297f60] FillArrays v1.5.0
[53c48c17] FixedPointNumbers v0.8.4
[59287772] Formatting v0.4.2
[f6369f11] ForwardDiff v0.10.36
[069b7b12] FunctionWrappers v1.1.3
[77dc65aa] FunctionWrappersWrappers v0.1.3
[d9f16b24] Functors v0.4.5
[46192b85] GPUArraysCore v0.1.5
[28b8d3ca] GR v0.72.9
[42e2da0e] Grisu v1.0.2
[cd3eb016] HTTP v1.9.14
[34004b35] HypergeometricFunctions v0.3.23
[22cec73e] InitialValues v0.3.1
[505f98c9] InplaceOps v0.3.0
[a98d9a8b] Interpolations v0.14.7
[8197267c] IntervalSets v0.7.7
[3587e190] InverseFunctions v0.1.12
[41ab1584] InvertedIndices v1.3.0
[92d709cd] IrrationalConstants v0.2.2
[c8e1da08] IterTools v1.8.0
[82899510] IteratorInterfaceExtensions v1.0.0
[1019f520] JLFzf v0.1.5
[692b3bcd] JLLWrappers v1.4.1
[682c06a0] JSON v0.21.4
[63c18a36] KernelAbstractions v0.9.8
[5ab0869b] KernelDensity v0.6.7
[929cbde3] LLVM v6.1.0
[8ac3fa9e] LRUCache v1.4.1
[b964fa9f] LaTeXStrings v1.3.0
[23fbe1c1] Latexify v0.16.1
[50d2b5c4] Lazy v0.15.1
[1d6d02ad] LeftChildRightSiblingTrees v0.2.0
[6f1fad26] Libtask v0.8.6
[6fdf6af0] LogDensityProblems v2.1.1
[996a588d] LogDensityProblemsAD v1.6.1
[2ab3a3ac] LogExpFunctions v0.3.24
[e6f89c97] LoggingExtras v1.0.0
[c7f686f2] MCMCChains v6.0.3
[be115224] MCMCDiagnosticTools v0.3.5
[e80e1ace] MLJModelInterface v1.8.0
[1914dd2f] MacroTools v0.5.10
[dbb5928d] MappedArrays v0.4.2
[739be429] MbedTLS v1.1.7
[442fdcdd] Measures v0.3.2
[128add7d] MicroCollections v0.1.4
[e1d29d7a] Missings v1.1.0
[6f286f6a] MultivariateStats v0.10.2
[872c559c] NNlib v0.9.4
[77ba4419] NaNMath v1.0.2
[86f7a689] NamedArrays v0.9.8
[c020b1a1] NaturalSort v1.0.0
[b8a86587] NearestNeighbors v0.4.13
[510215fc] Observables v0.5.4
[6fe1bfb0] OffsetArrays v1.12.10
[4d8831e6] OpenSSL v1.4.1
[3bd65402] Optimisers v0.2.19
[bac558e1] OrderedCollections v1.6.2
[90014a1f] PDMats v0.11.17
[69de0a69] Parsers v2.7.2
[b98c9c47] Pipe v1.3.0
[ccf2f8ad] PlotThemes v3.1.0
[995b91a9] PlotUtils v1.3.5
[91a5bcdd] Plots v1.38.17
[aea7be01] PrecompileTools v1.1.2
[21216c6a] Preferences v1.4.0
[08abe8d2] PrettyTables v2.2.7
[33c8b6b6] ProgressLogging v0.1.4
[92933f4c] ProgressMeter v1.7.2
[1fd47b50] QuadGK v2.8.2
[74087812] Random123 v1.6.1
[e6cf234a] RandomNumbers v1.5.3
[b3c3ace0] RangeArrays v0.3.2
[c84ed2f1] Ratios v0.4.5
[c1ae055f] RealDot v0.1.0
[3cdcf5f2] RecipesBase v1.3.4
[01d81517] RecipesPipeline v0.6.12
[731186ca] RecursiveArrayTools v2.38.7
[189a3867] Reexport v1.2.2
[05181044] RelocatableFolders v1.0.0
[ae029012] Requires v1.3.0
[79098fc4] Rmath v0.7.1
[f2b01f46] Roots v2.0.17
[7e49a35a] RuntimeGeneratedFunctions v0.5.12
[0bca4576] SciMLBase v1.94.0
[c0aeaf25] SciMLOperators v0.3.6
[30f210dd] ScientificTypesBase v3.0.0
[6c6a2e73] Scratch v1.2.0
[91c51154] SentinelArrays v1.4.0
[efcf1570] Setfield v1.1.1
[992d4aef] Showoff v1.0.3
[777ac1f9] SimpleBufferStream v1.1.0
[ce78b400] SimpleUnPack v1.1.0
[a2af1166] SortingAlgorithms v1.1.1
[276daf66] SpecialFunctions v2.3.0
[171d559e] SplittablesBase v0.1.15
[90137ffa] StaticArrays v1.6.2
[1e83bf80] StaticArraysCore v1.4.2
[64bff920] StatisticalTraits v3.2.0
[82ae8749] StatsAPI v1.6.0
[2913bbd2] StatsBase v0.34.0
[4c63d2b9] StatsFuns v1.3.0
[f3b207a7] StatsPlots v0.15.6
[892a3eda] StringManipulation v0.3.0
[09ab397b] StructArrays v0.6.15
[2efcf032] SymbolicIndexingInterface v0.2.2
[ab02a1b2] TableOperations v1.2.0
[3783bdb8] TableTraits v1.0.1
[bd369af6] Tables v1.10.1
[62fd8b95] TensorCore v0.1.1
[5d786b92] TerminalLoggers v0.1.7
[9f7883ad] Tracker v0.2.26
[3bb67fe8] TranscodingStreams v0.9.13
[28d57a85] Transducers v0.4.78
[410a4b4d] Tricks v0.1.7
[781d530d] TruncatedStacktraces v1.4.0
[fce5fe82] Turing v0.28.1
[5c2747f8] URIs v1.5.0
[1cfade01] UnicodeFun v0.4.1
[1986cc42] Unitful v1.16.2
[45397f5d] UnitfulLatexify v1.6.3
[013be700] UnsafeAtomics v0.2.1
[d80eeb9a] UnsafeAtomicsLLVM v0.1.3
[41fe7b60] Unzip v0.2.0
[cc8bc4a8] Widgets v0.6.6
[efce3f68] WoodburyMatrices v0.5.5
[700de1a5] ZygoteRules v0.2.3
⌅ [68821587] Arpack_jll v3.5.1+1
[6e34b625] Bzip2_jll v1.0.8+0
[83423d85] Cairo_jll v1.16.1+1
[2e619515] Expat_jll v2.5.0+0
⌃ [b22a6f82] FFMPEG_jll v4.4.2+2
[f5851436] FFTW_jll v3.3.10+0
[a3f928ae] Fontconfig_jll v2.13.93+0
[d7e528f0] FreeType2_jll v2.13.1+0
[559328eb] FriBidi_jll v1.0.10+0
[0656b61e] GLFW_jll v3.3.8+0
[d2c73de3] GR_jll v0.72.9+1
[78b55507] Gettext_jll v0.21.0+0
[7746bdde] Glib_jll v2.74.0+2
[3b182d85] Graphite2_jll v1.3.14+0
[2e76f6c2] HarfBuzz_jll v2.8.1+1
[1d5cc7b8] IntelOpenMP_jll v2023.2.0+0
[aacddb02] JpegTurbo_jll v2.1.91+0
[c1c5ebd0] LAME_jll v3.100.1+0
[88015f11] LERC_jll v3.0.0+1
[dad2f222] LLVMExtra_jll v0.0.23+0
[1d63c593] LLVMOpenMP_jll v15.0.4+0
[dd4b983a] LZO_jll v2.10.1+0
⌅ [e9f186c6] Libffi_jll v3.2.2+1
[d4300ac3] Libgcrypt_jll v1.8.7+0
[7e76a0d4] Libglvnd_jll v1.6.0+0
[7add5ba3] Libgpg_error_jll v1.42.0+0
[94ce4f54] Libiconv_jll v1.16.1+2
[4b2f31a3] Libmount_jll v2.35.0+0
[89763e89] Libtiff_jll v4.5.1+1
[38a345b3] Libuuid_jll v2.36.0+0
[856f044c] MKL_jll v2023.2.0+0
[e7412a2a] Ogg_jll v1.3.5+1
⌅ [458c3c95] OpenSSL_jll v1.1.22+0
[efe28fd5] OpenSpecFun_jll v0.5.5+0
[91d4177d] Opus_jll v1.3.2+0
[30392449] Pixman_jll v0.42.2+0
[c0090381] Qt6Base_jll v6.4.2+3
[f50d1b31] Rmath_jll v0.4.0+0
[a2964d1f] Wayland_jll v1.21.0+0
[2381bf8a] Wayland_protocols_jll v1.25.0+0
[02c8fc9c] XML2_jll v2.10.3+0
[aed1982a] XSLT_jll v1.1.34+0
[ffd25f8a] XZ_jll v5.4.4+0
[4f6342f7] Xorg_libX11_jll v1.8.6+0
[0c0b7dd1] Xorg_libXau_jll v1.0.11+0
[935fb764] Xorg_libXcursor_jll v1.2.0+4
[a3789734] Xorg_libXdmcp_jll v1.1.4+0
[1082639a] Xorg_libXext_jll v1.3.4+4
[d091e8ba] Xorg_libXfixes_jll v5.0.3+4
[a51aa0fd] Xorg_libXi_jll v1.7.10+4
[d1454406] Xorg_libXinerama_jll v1.1.4+4
[ec84b674] Xorg_libXrandr_jll v1.5.2+4
[ea2f1a96] Xorg_libXrender_jll v0.9.10+4
[14d82f49] Xorg_libpthread_stubs_jll v0.1.1+0
[c7cfdc94] Xorg_libxcb_jll v1.15.0+0
[cc61e674] Xorg_libxkbfile_jll v1.1.2+0
[12413925] Xorg_xcb_util_image_jll v0.4.0+1
[2def613f] Xorg_xcb_util_jll v0.4.0+1
[975044d2] Xorg_xcb_util_keysyms_jll v0.4.0+1
[0d47668e] Xorg_xcb_util_renderutil_jll v0.3.9+1
[c22f9ab0] Xorg_xcb_util_wm_jll v0.4.1+1
[35661453] Xorg_xkbcomp_jll v1.4.6+0
[33bec58e] Xorg_xkeyboard_config_jll v2.39.0+0
[c5fb5394] Xorg_xtrans_jll v1.5.0+0
[3161d3a3] Zstd_jll v1.5.5+0
⌅ [214eeab7] fzf_jll v0.29.0+0
[a4ae2306] libaom_jll v3.4.0+0
[0ac62f75] libass_jll v0.15.1+0
[f638f0a6] libfdk_aac_jll v2.0.2+0
[b53b4c65] libpng_jll v1.6.38+0
[f27f6e37] libvorbis_jll v1.3.7+1
[1270edf5] x264_jll v2021.5.5+0
[dfaa095f] x265_jll v3.5.0+0
[d8fb68d0] xkbcommon_jll v1.4.1+0
[0dad84c5] ArgTools v1.1.1
[56f22d72] Artifacts
[2a0f44e3] Base64
[ade2ca70] Dates
[8ba89e20] Distributed
[f43a241f] Downloads v1.6.0
[7b1f6079] FileWatching
[9fa8497b] Future
[b77e0a4c] InteractiveUtils
[4af54fe1] LazyArtifacts
[b27032c2] LibCURL v0.6.3
[76f85450] LibGit2
[8f399da3] Libdl
[37e2e46d] LinearAlgebra
[56ddb016] Logging
[d6f4376e] Markdown
[a63ad114] Mmap
[ca575930] NetworkOptions v1.2.0
[44cfe95a] Pkg v1.9.2
[de0858da] Printf
[3fa0cd96] REPL
[9a3f8284] Random
[ea8e919c] SHA v0.7.0
[9e88b42a] Serialization
[1a1011a3] SharedArrays
[6462fe0b] Sockets
[2f01184e] SparseArrays
[10745b16] Statistics v1.9.0
[4607b0f0] SuiteSparse
[fa267f1f] TOML v1.0.3
[a4e569a6] Tar v1.10.0
[8dfed614] Test
[cf7118a7] UUIDs
[4ec0a83e] Unicode
[e66e0078] CompilerSupportLibraries_jll v1.0.5+0
[deac9b47] LibCURL_jll v7.84.0+0
[29816b5a] LibSSH2_jll v1.10.2+0
[c8ffd9c3] MbedTLS_jll v2.28.2+0
[14a3606d] MozillaCACerts_jll v2022.10.11
[4536629a] OpenBLAS_jll v0.3.21+4
[05823500] OpenLibm_jll v0.8.1+0
[efcefdf7] PCRE2_jll v10.42.0+0
[bea87d4a] SuiteSparse_jll v5.10.1+6
[83775a58] Zlib_jll v1.2.13+0
[8e850b90] libblastrampoline_jll v5.8.0+0
[8e850ede] nghttp2_jll v1.48.0+0
[3f19e933] p7zip_jll v17.4.0+0
Info Packages marked with ⌃ and ⌅ have new versions available, but those with ⌅ are restricted by compatibility constraints from upgrading. To see why use `status --outdated -m`